prml第九章

EM算法

期望最大化（EM）算法，是寻找具有潜在变量的概率模型的最大似然解的一种通用方法。
我们希望能对观测变量进行建模，但是我们一般会遇到无法对观测变量直接建模，需要引入隐含变量，用含有隐藏变量的分布来建模。比如说高斯分布是单峰的，虽然很灵活但对多峰分布等情况不能很好的近似，有很大的局限性。但是引入潜在变量变成混合高斯就可以解决他的局限性。考虑一个概率模型有观测变量X和隐含变量Z。他们联合概率分布$p(x,z \vert \theta)$由参数$\theta$控制。我们目标是找一组参数$\theta$使观测到的结果$x$最大。就是要最大化对数似然函数$\ln p(x\vert \theta)$。由于隐含变量Z的存在，我们关于$\theta$最优化$p(x\vert \theta)$一般很困难(涉及到对数里面有求和)：

$$\ln p(x\vert \theta) = \ln \int_z p(x,z \vert \theta) dz$$

我们引入潜在变量分$q(x)$和Jensen不等式（见prml1.2）lnx是上凸函数有$f(E(x)) \geq E(f(x))$。

$$\begin{aligned} \ln p(x\vert \theta) &= \ln \int_z p(x,z \vert \theta)dz\\&= \ln \int_z q(z)\frac{p(x,z \vert \theta)}{q(z)}dz \\& = \ln (E_{q(z)}[\frac{p(x,z \vert \theta)}{q(z)}]) \\ & \geq E_{q(z)}[\ln \frac{p(x,z \vert \theta)}{q(z)}] =ELBO \end{aligned}$$

ELBO是证据下界（Evidence Lower Bound）。
当$\frac{p(x,z \vert \theta)}{q(z)}$是常数时等式成立。

$$\begin{aligned} c &= \frac{p(x,z \vert \theta)}{q(z)} \\ \int_zcq(z)dz &= \int_zp(x,z\vert \theta)dz \\c &= p(x \vert\theta)\\ q(z) &= \frac{p(x,z \vert \theta)}{p(x \vert\theta)} = p(z \vert x,\theta) \end{aligned}$$

即得到狭义的EM算法：
选择$q(z)$使下界$ELBO$等于对数似然函数$\ln p(x \vert \theta)$，然后关于$\theta$最大化下界ELBO。得到的新的$\theta$对应的ELBO就能大于旧的$\theta$对应的ELBO，这样新的对数似然$\ln p(x\vert \theta)$大于旧的$\ln p(x\vert \theta)$。从而使对数似然函数变大。

E步骤：
找到$q(z) = p(z \vert x,\theta^*)$
M步骤：

$$\begin{aligned} \theta^* &= \arg\max_{\theta} (E_{q(z)}[\ln \frac{p(x,z \vert \theta)}{q(z)}])\\ & = \arg\max_{\theta} (E_{q(z)}[\ln p(x,z \vert \theta)]) \end{aligned}$$

考虑以下分解方法(引入潜在变量分布q(x)，想办法凑出上面我们得到的下界):

$$\begin{aligned} \ln p(x\vert \theta) &= \ln p(x,z \vert \theta) - \ln p(z \vert x, \theta)\\ & = \ln \frac{p(x,z \vert \theta)}{q(z)} - \ln \frac{p(z \vert x, \theta)}{q(z)}\\ & = E_{q(z)}[\ln \frac{p(x,z \vert \theta)}{q(z)}] - E_{q(z)}[\ln \frac{p(z \vert x, \theta)}{q(z)}]\\ & = ELBO + KL(q \vert \vert p) \end{aligned}$$

$KL()$为两个函数之间的KL散度，用来描述两个函数之间的相似性，KL散度一定大于0。（KL散度描述见prml1.2）
相当于ELBO和对数似然之间的距离是$q(z)$和$p(z \vert x, \theta)$之间的KL散度。即对数似然等于ELBO加KL散度。
这样可以得到一般化的EM算法。与狭义的E步骤不同，当我们无法得到$p(z \vert x, \theta)$时，我们可以令已知的分布$q(z)$去逼近$p(z \vert x, \theta)$。即令KL散度最小。
E步骤：

$$q = \arg\min_{q}KL(q \vert \vert p)$$

M步骤：

$$\theta^* = \arg\max_{\theta} (E_{q(z)}[\ln \frac{p(x,z \vert \theta)}{q(z)}])$$

高斯混合模型

高斯混合模型是将多个的高斯分布进行线性叠加的概率模型。他认为得到的数据分为好多类，每一类服从特定均值和方差的高斯分布。他能更好的描述多峰的分布。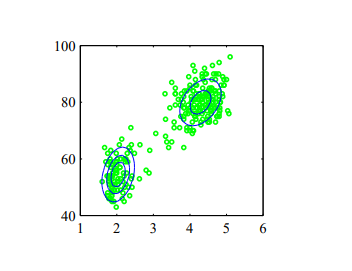

上图可以看到，数据集($x_1,x_2…x_n…x_N$)（绿色数据点）主要聚集成两类，混合高斯模型可以很好的拟合。
假设我们有数据集($x_1,x_2…x_n…x_N$)，引入各聚类的均值$\mu_k$和方差$\Sigma_k$。高斯混合模型的边缘概率密度：

$$p(x_n \vert \pi,\mu,\Sigma) = \sum_{k = 1}^K \pi_k N(x_n \vert \mu_k,\Sigma_k)$$

引入n个K维的二值随机隐含变量$z_n$，每一个$z_n$中只有一个特殊的$z_{nk}$等于1其余为0。他来描述第n个数据被分为哪一类，若$z_{nk}= 1$则说明第n个数据$\mathbf x_n$属于第k类，$z_n$服从多项式分布。

$$\begin{aligned} &p(z_{nk} = 1) = \pi_k &\sum_k^K \pi_k = 1 \end{aligned}$$

$z_{nk} = 1$时第n个数据点数据点$x_n$被分为k类，服从$\mu_k,\Sigma_k$的高斯分布。就是说似然函数是：

$$p(x_n \vert z_{nk} = 1) = N(x_n \vert \mu_k,\Sigma_k)$$

那么我们可以求到$z$的后验分布：

$$\begin{aligned} p(z_{nk} = 1 \vert x_n) &= \frac{p(x_n \vert z_{nk} = 1)p(z_{nk} = 1)}{p(x_n)}\\ & = \frac{\pi_kN(x_n \vert \mu_k,\Sigma_k)}{\sum_{j = 1}^K \pi_j N(x_n \vert \mu_j,\Sigma_j)} \end{aligned}$$

多维高斯分布有：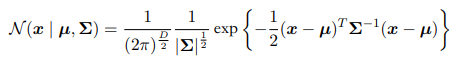

完整对数似然函数是：

$$\begin{aligned} \ln p(\mathbf{x},\mathbf{z} \vert \pi,\mu,\Sigma) &= \ln \prod_{n=1}^N \prod_{k=1}^K (\pi_kN(x_n \vert \mu_k,\Sigma_k))^{z_{nk}}\\& = \sum_{n=1}^N\sum_{k=1}^K z_{nk} (\ln \pi_k N(x_n \vert \mu_k,\Sigma_k))\\& = \sum_{n=1}^N\sum_{k=1}^K z_{nk} (\ln \pi_k -\frac{1}{2}(x_n - \mu_k)^T\Sigma_k^{-1}(x_n - \mu_k)-\frac{1}{2} \ln \vert \Sigma_k \vert) +C \end{aligned}$$

C是与参数无关的常数；ELBO为：

$$\begin{aligned} &E_{q(z)}[\ln p(\mathbf{x},\mathbf{z} \vert \pi,\mu,\Sigma)]= E_{q(z)}[\sum_{n=1}^N\sum_{k=1}^K z_{nk} (\ln \pi_k -\frac{1}{2}(x_n - \mu_k)^T\Sigma_k^{-1}(x_n - \mu_k)-\frac{1}{2} \ln \vert \Sigma_k \vert) + C ] \\ & = \sum_{n=1}^N\sum_{k=1}^K q(z_{nk} = 1) (\ln \pi_k -\frac{1}{2}(x_n - \mu_k)^T\Sigma_k^{-1}(x_n - \mu_k)-\frac{1}{2} \ln \vert \Sigma_k \vert) + C \end{aligned}$$

对各参数（$\mu_k,\Sigma_k$）求导:
对$\mu_k,\Sigma_k$求导会遇到二项式求导的问题：

$$\alpha = X^T A X = \sum^n_{j}\sum^n_{i}a_{ij}x_ix_j$$ $$\frac{\partial\alpha}{\partial x_k} = \sum_{i \neq k}^n a_{ik}x_i + \sum_{j \neq k}^n a_{kj}x_j + 2*a_{kk}x_k = \sum_{i}^n a_{ik}x_i + \sum_{j}^n a_{kj}x_j$$ $$\frac{\partial(X^T A X)}{X} = A^T X + A X$$

用上面得到的结论：

$$\mu_k = \frac{\sum_{n= 1}^N q(z_{nk} = 1)*x_n}{\sum_{n= 1}^N q(z_{nk} = 1)} = \frac{1}{N_k} [q(z_{nk} = 1)*x_n]$$

$N_k = \sum_{n= 1}^N q(z_{nk} = 1)$；对$\Sigma_k$求导时，会遇到对行列式求导的问题：
求矩阵行列式

$$\vert A\vert = A_{ij}C_{ij}$$

$C_{ij}$是矩阵$A$元素$A_{ij}$的代数余子式；我们知道$A$的伴随矩阵是由$A$各元素的代数余子式构成的。即：

$$A^{*}_{ij} = C_{ji}$$

所以有：

$$\frac{\partial \vert A \vert}{\partial A_{ij}} = A^*_{ji}$$

即

$$\frac{\partial \vert A \vert}{\partial A} = (A^*)^T$$

若$A$可逆有$A^* = \vert A \vert A^{-1}$

$${(\ln \vert A \vert)}^\prime = (A^{-1})^T$$

同时还会遇到以下导数:

$$\frac{\partial (X^T A^{-1}X)}{\partial A}$$

要求这个需要先引入对$A^{-1}$的导数：

$$\begin{aligned} 0 &= \frac{\partial I}{\partial x} = \frac{\partial (AA^{-1})}{\partial x}\\ 0 &= A \frac{\partial (A^{-1})}{\partial x} + A^{-1}\frac{\partial A}{\partial x}\\ \frac{\partial (A^{-1})}{\partial x} &= -A^{-1}\frac{\partial A}{\partial x}A^{-1} \end{aligned}$$ $$\begin{aligned} \frac{\partial (X^T A^{-1}X)}{\partial a_{ij}} &= -X^TA^{-1}\frac{\partial A}{\partial a_{ij}}A^{-1}X = X^TA^{-1}I_{ij}A^{-1}X \\ &= (X^T A^{-1}_{:i})(A^{-1}_{:j}X) \end{aligned}$$

$I_{ij}$是一个n*n矩阵只有第$i$行第$j$列是1，其余位置是0。可以看图理解：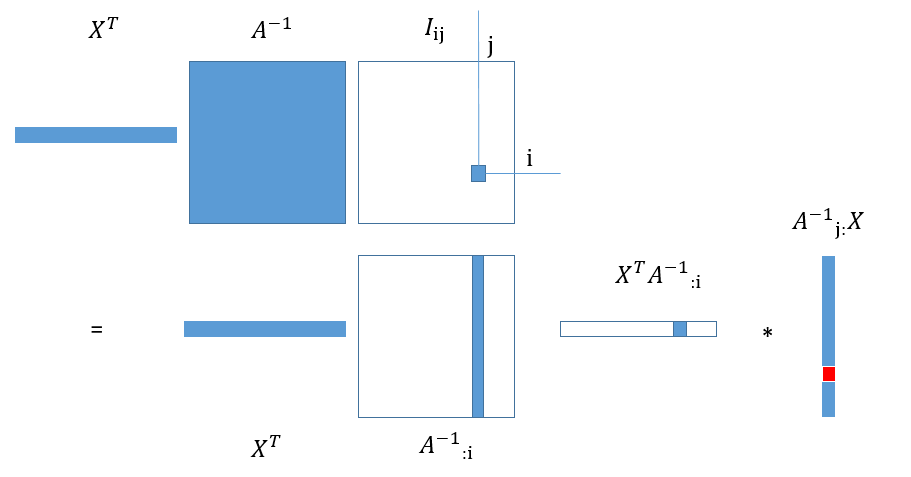

然后我们要扩展成对矩阵求导（将上述两向量交换相乘顺序，既可以得到导数矩阵的转置）：

$$\frac{\partial (X^T A^{-1}X)}{\partial A} = (A^{-1}XX^TA^{-1})^T = (A^{-1})^TXX^T(A^{-1})^T$$

运用上述结论，即可以得到：

$$\begin{aligned} &\sum_{n=1}^N q(z_{nk} = 1)((\Sigma_k^{-1})^T(x_n-\mu_k)(x_n-\mu_k)^T(\Sigma_k^{-1})^T - (\Sigma_k^{-1})^T) = 0\\ &\Sigma_k = \frac{\sum_{n=1}^N q(z_{nk} = 1)(x_n-\mu_k)(x_n-\mu_k)^T}{N_k} \end{aligned}$$

对$\pi_k$最大化需引入$\sum_k \pi_k = 1$的限制条件，用拉格朗日乘数法进行优化。

$$\sum_n^{N}\frac{q(z_{nk} = 1)}{\pi_k} + \lambda = 0$$ $$\sum_k \pi_k = 1$$ $$\lambda = - \sum_k^K\sum_n^{N}q(z_{nk} = 1) = -N$$ $$\pi_k = \frac{N_K}{N}$$

其中有$N = \sum_k^K\sum_n^{N}q(z_{nk} = 1)$。
这样我们就可以得到EM算法用于高斯混合模型的具体流程：
E步骤：
计算旧参数对应的后验分布q:

$$q(z_{nk} = 1) = p(z_{nk} = 1 \vert x_n) = \frac{\pi_kN(x_n \vert \mu_k,\Sigma_k)}{\sum_{j = 1}^K \pi_j N(x_n \vert \mu_j,\Sigma_j)}$$

M步骤:
更新参数：

$$\mu_k = \frac{1}{N_k} q(z_{nk} = 1)*x_n$$ $$\Sigma_k = \frac{\sum_{n=1}^N q(z_{nk} = 1)(x_n-\mu_k)(x_n-\mu_k)^T}{N_k}$$ $$\pi_k = \frac{N_K}{N}$$

其中：$N = \sum_k^K\sum_n^{N}q(z_{nk} = 1)$，$N_k = \sum_{n= 1}^N q(z_{nk} = 1)$
笼统地说，这个具体流程像是先确定几个中心点，然后第一步先求各个数据点属于每一类的概率，再以这个概率为权重求均值和方差，让数据点来更改中心点，就这样一步步迭代最后给各数据点聚类（这里的聚类用概率来表示，不是说这个数据点属于哪一类，而是说数据点属于各类的概率，是一种”软”聚类。），并得到与数据点拟合的高斯混合概率模型。

k均值聚类

假设有数据集($x_1,x_2…x_n…x_N$)，同时引入k个聚类中心$\mu_k$,k均值聚类目的是令以下J最小：

$$J = r_{nk}*\vert\vert x_n - \mu_k \vert\vert^2$$

$r_{nk}$是分类的指示器，$r_{nk} = 1$证明数据$x_n$属于$k$类。
他的迭代方法也类似与EM算法两部分，只是他的后验概率比较特殊。
E步骤：

$$r_{nk} = 1 (k = \arg\min_k \vert\vert x_n - \mu_k \vert\vert^2)$$

M步骤：
更新参数$\mu_k = \frac{\sum_n r_{nk} * x_n}{\sum_n r_{nk}}$
K均值聚类其实是一种特殊的高斯混合模型。他将方差矩阵固定设置为$\epsilon I$，并让$\epsilon \to 0$。这样后验分布就变成：

$$p(z_{nk} = 1 \vert x_n) = \frac{\pi_k \exp(-\frac{\vert\vert x_n - \mu_k \vert\vert^2}{2\epsilon})}{\sum_{j = 1}^K \pi_j \exp(-\frac{\vert\vert x_n - \mu_j \vert\vert^2}{2\epsilon})} = r_{nk}$$

$\epsilon \to 0$时，相当于给$\vert\vert x_n - \mu_k \vert\vert^2$乘上一个很大的值。假如说$\vert\vert x_n - \mu_j \vert\vert^2 > \vert\vert x_n - \mu_k \vert\vert^2$，稍微大一点就会被$\epsilon$扩大到大很多。然后再求负指数，负指数内值越大，得到的指数就越小。这样$\exp(-\frac{\vert\vert x_n - \mu_j \vert\vert^2}{2\epsilon}) <<\exp(-\frac{\vert\vert x_n - \mu_k \vert\vert^2}{2\epsilon})$。相当于只要$\vert\vert x_n - \mu_k \vert\vert^2$不是最小的，他就会给放的很小直到可以忽略，只有最小的可以留下。这样只有$k = \arg\min_k \vert\vert x_n - \mu_k \vert\vert^2$可以令$p(z_{nk} = 1 \vert x_n) = 1$即第二个等号成立。他的后验概率只能取0和1，相当于每一个样本只可能是某一类。是一种“硬”分类。同时只估计了均值而没有更新方差。

伯努利混合模型

我们考虑一个伯努利分布的混合模型，这种模型也被称为潜在类别分析。数据$\mathbf{x}$是有D个二值变量$x_i$组成的向量，变量$x_i$服从参数为$\mu_i$伯努利分布。即：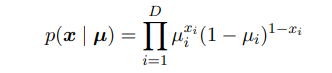

然后我们考虑这种分布的有限混合：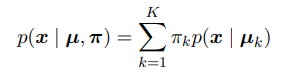

其中$\mathbf{x} = (x_1,..x_D)$,$\mathbf{\mu_k} = (\mu_1,..\mu_i..\mu_D)$
假如我们有一数据集$\mathbf{X} = (\mathbf{x}_1…\mathbf{x}_N)$，那么我们可以得到这个模型的对数似然函数：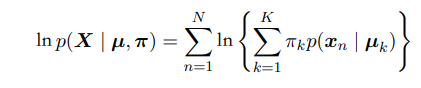

可以看到对数内有求和使得最大似然解没有解析解。与高斯分布相同我们引入n个K维的二值隐含变量$z_n$，每一个$z_n$中只有一个特殊的$z_{nk}$等于1其余为0。他来描述第n个数据被分为哪一类，若$z_{nk}= 1$则说明第n个数据$\mathbf{x_n}$属于第k类。$z_n$服从多项式分布。我们使用EM算法。
E步骤（求后验）：

$$p(x_n \vert z_{nk} = 1,\mu) = p(x_n \vert \mu_k)$$ $$p(z_{nk} = 1) = \pi_k$$

自然可以得到后验：

$$p(z_{nk} = 1) = \frac{\pi_k p(x_n \vert \mu_k)}{\sum_{j = 1}^K \pi_j p(x_n \vert \mu_j)}$$

M步骤（最大化下界）：
完整数据的对数似然：

$$\begin{aligned} \ln p(\mathbf{x},\mathbf{z} \vert \pi,\mu) &= \ln \prod_{n=1}^N \prod_{k=1}^K (p(x_n \vert z_{nk})p(z_{nk} ))^{z_{nk}}\\& = \sum_{n=1}^N\sum_{k=1}^K z_{nk} (\ln \pi_k p(x_n \vert \mu_k))\\& = \sum_{n=1}^N\sum_{k=1}^K z_{nk} (\ln \pi_k + \sum_i^D[x_{ni}\ln\mu_{ki}+(1-x_{ni})\ln(1-\mu_{ki})]) \end{aligned}$$

下界：

$$\begin{aligned} &E_{q(z)}[\sum_{n=1}^N\sum_{k=1}^K z_{nk}(\ln \pi_k + \sum_i^D[x_{ni}\ln\mu_{ki}+(1-x_{ni})\ln(1-\mu_{ki})]) ] \\ & = \sum_{n=1}^N\sum_{k=1}^K q(z_{nk} = 1) (\ln \pi_k + \sum_i^D[x_{ni}\ln\mu_{ki}+(1-x_{ni})\ln(1-\mu_{ki})]) \end{aligned}$$

对各参数求导，或采用拉格朗日乘数法可以得到以下结果。

$$\mu_k = \frac{1}{N_k}\sum_n q(z_{nk} = 1)\mathbf{x}_n$$ $$\pi_k = \frac{N_k}{N}$$

其中：$N = \sum_k^K\sum_n^{N}q(z_{nk} = 1)$，$N_k = \sum_{n= 1}^N q(z_{nk} = 1)$
我们可以使用伯努利混合模型对二值化的数字图像进行建模后聚类。其中$x_n$就是各二值化后的图像，得到的潜在变量$z_{nk}$的后验概率则为聚类结果。得到的$\mu_k$则可以看作是各数字的图像的概率分布（就是该算法认为的数字长得样子）。