这一章公式有点多，把爷麻了，下次搞点别的

共轭分布

二项分布

假设一个随机变量只会取0或1两个可能的值，如投掷硬币正面计1反面计0，假若正面概率是$\mu$,做N次实验，m次为正面的概率就是二项分布：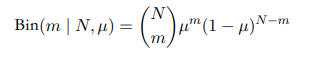

其中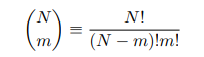

是N个选出m个方式的总数，是归一化系数。
此时我们如果抛了N次得到m次正面，想要估计这个二项分布；
我们对这个概率取对数得到：

$$mln\mu+(N-m)ln(1-\mu)+C$$

求导令其为零得到最大似然估计值$\mu = \frac m N$。
假如你非常非，投了N次都是反面那你$\mu = 0$，也就是说你的模型认为不会投到正面。就会出现之前提到的最大似然会产生过拟合的结果。贝叶斯观点需要引入一个先验概率分布$p(\mu)$和这个$p(m \vert \mu)$相乘得到后验分布$p(\mu \vert m)$就可以避免过拟合；怎么选择先验分布？我们希望选择的先验分布乘了似然函数之后还保持原来的函数形式，这样我们得到的后验分布就可以用为下一次训练的先验概率分布。这时我们就称这个先验函数是似然函数的共轭分布。
二项分布的一个共轭分布为贝塔分布。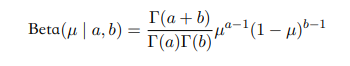

这个分布是关于$\mu$的，$\Gamma(x) = \int _0 ^\infty t^{x-1}e^{-t}dt$是伽马函数。前面$\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}$是归一化参数，是为了让整体分布对$\mu$积分为1。证明：

$$\begin{aligned} \Gamma(a)\Gamma(b) &= \int_{0}^{\infty}\int_{0}^{\infty}e^{-(x+y)}x^{a-1}y^{b-1}dxdy\\ &= \int_{0}^{\infty}x^{a-1}dx\int_{x}^{\infty}e^{-t}(t-x)^{b-1}dt &(x+y = t)\\ & = \int_{0}^{1}(t\mu)^{a-1}(t-t\mu)^{b-1}td\mu\int_{0}^{\infty}e^{-t}dt &(x = t\mu) \\& = \Gamma(a+b)\int_{0}^{1}\mu^{a-1}(1-\mu)^{b-1}d\mu \end{aligned}$$

贝塔分布的期望：

$$\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\int_0^1\mu^{a}(1-\mu)^{b-1}d\mu = \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}*\frac{\Gamma(a+1)\Gamma(b)}{\Gamma(a+b+1)} = \frac{a}{a+b}$$

我们可以发现贝塔函数乘以二项分布得到的后验分布仍然是贝塔分布。

$$Bin(m \vert N,\mu)*Beta(\mu \vert a,b) \propto \mu^{a+m-1}(1-\mu)^{b+l-1}$$

$l = N-m$，该贝塔分布参数变为$(a+m-1,b+l-1)$。该数据集中有m个实验结果为1，l个实验结果为0，从先验概率到后验概率，a的值变⼤了m，b的值变⼤了l。然后变化后的参数又可以作为新的先验的新的a,b。可以简单地把先验概率中的超参数a和b分别看成x = 1和x = 0的有效观测数。
我们可以用贝塔分布来预测下一次实验的输出：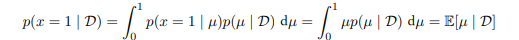


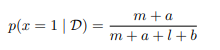
以硬币举例子，你一开始的先验信息正反面是一样的假设$a = b = 2$。正面的概率是0.5。然后你做一波实验得到4次正面0次反面，你的$a=6,b=2$，正面的概率变成是0.75。然后这个a,b又可以作为新的先验的参数继续接收新的实验数据。

多项式分布

二项分布是投硬币，而多项式分布则像是投骰子，一个随机变量有可能取1，2，3…k。进行N次，每一个可选项分别为m1,m2,m3…mk的概率。

$$Mult(m1,m2,m3...mk \vert \mu,N) = \frac{N!}{m_1!m_2!...m_k!}*\prod _{j=1}^k \mu_j^{m_j}$$

归一化系数是把N分为个数m1,m2,m3…mk的k组的方案数。与二项分布同样的，我们可以得到多项式分布对应的共轭分布狄利克雷分布。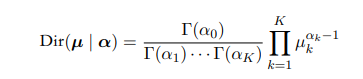


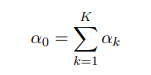
归一化系数证明可以参考贝塔分布归一化系数的证明。用似然函数多项式分布去乘上先验狄利克雷分布可以得到新的狄利克雷分布。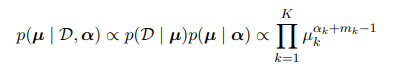

$m_k$对应实验数据中随机变量值为$k$时的次数，我们可以把狄利克雷分布的参数$\alpha_k$看成的随机变量值为$k$有效观测数。
平均来看，随着我们观测到越来越多的数据，后验概率表⽰的不确定性将会持续下降。考虑一个贝叶斯问题，参数为$\theta$,观测到一组数据$D$。由全期望公式有：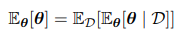

我们可以证明：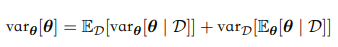

平均来看，θ的后验方差小于先验方差。后验均值的方差越⼤，这个方差的减小就越⼤。
证明：

$$\begin{aligned} E_D[var_\theta[\theta \vert D]] &=\int (E^2_\theta[\theta \vert D]-(E_\theta[\theta \vert D])^2 )p(D) dD\\&= E^2_\theta[\theta]-\int(E_\theta[\theta \vert D])^2 p(D) dD\\ var_D[E_\theta[\theta \vert D]] &=\int(E_\theta[\theta \vert D])^2 p(D) dD - (\int(E_\theta[\theta \vert D]) p(D) dD)^2\\&=\int(E_\theta[\theta \vert D])^2 p(D) dD - (E_\theta[\theta])^2\\ var_\theta[\theta]&= E^2_\theta[\theta] - (E_\theta[\theta])^2 \end{aligned}$$

高斯分布

多元高斯分布

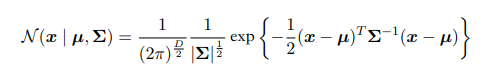
其中，$\mu$是D维均值向量，$\Sigma$是$D \times D$协方差矩阵，$\vert \Sigma \vert$是$\Sigma$的行列式。高斯函数对与x的依赖取决于下面的二次型: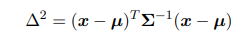

我们可以求得该矩阵$\Sigma$特征值$\lambda_i$和与之对应的特征向量$u_i$，$i=1,2,3…D$。$\Sigma^{-1}$的特征值就为$\frac{1}{\lambda_i}$,对应的标准化单位化后的特征向量为$u_i$。我们可以将该二次型变换为标准二次型。标准二次型矩阵对角线值为原二次型特征值$\frac{1}{\lambda_i}$。进行的变换为:

$$\begin{aligned} y &= U(x-\mu) & U =(u_1,u_2...u_i) \end{aligned}$$

经过上述变换可以将一个多元高斯分布变成多个独立的一元高斯分布。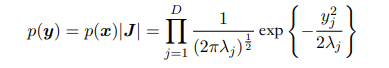

$\vert J\vert$是Jacobian（雅可比）行列式，元素为 $U_{ij}$ ，由于U是标准化单位化的特征向量组成的所以可以得到 $\vert J\vert = 1$ 。

多元高斯分布均值和方差

多元高斯分布的均值：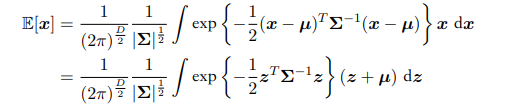

奇函数在正负无穷的积分为0，同时多元高斯分布积分在正负无穷积分为1，故多元高斯分布均值：

$$E[x] = \mu$$

所以$\mu$称为多元高斯分布的均值向量。

多元高斯分布的方差：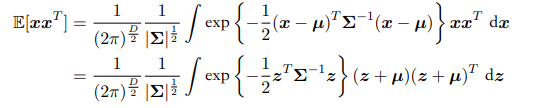

$$\begin{aligned} Var[x] &= E[xx^T] - E[x](E[x])^T = E[xx^T] - \mu\mu^T\\ &= \frac{1}{C}\int exp(-\frac{1}{2}z^T \Sigma^{-1}z)zz^Tdz \\&= \frac{1}{C}\int exp(-\frac{1}{2}z^T \Sigma^{-1}z)U^TUzz^TU^TU\vert J\vert dy \\&= \frac{1}{C}U^T\int exp(-\frac{1}{2}y^Tdiag(1/\lambda)y)y^Tydy U \\& = U^Tdiag(\lambda)U = \Sigma \end{aligned}$$

$diag(*)$是将括号内的向量作为对角线的元素的对角矩阵，其余元素为0。
最后一步的积分是这样计算的：

$$\begin{aligned} A&=\frac{1}{C} \int exp(-\frac{1}{2}y^Tdiag(1/\lambda)y)y^Tydy\\ A[i,i] & = \frac{1}{C^\prime}\int exp(-\frac{y_i^2}{2\lambda})y_i^2dy_i = \lambda\\ A[i,j] & = \frac{1}{C^\prime}\int\int exp(-\frac{y_i^2}{2\lambda}-\frac{y_j^2}{2\lambda})y_iy_jdy_idy_j = 0 \end{aligned}$$

所以$\Sigma$称为多元高斯分布的协方差矩阵。

高斯分布局限性

我们考虑用高斯分布去作为一个概率密度模型，会遇到以下问题

• 协方差矩阵自由参数过多，参数个数是维度的平方，求逆等运算麻烦，我们考虑限制协方差矩阵的自由参数，使其只能有对角线元素，但这样会限制这个模型的自由度从而限制表达能力。
• 高斯分布是单峰的，不能很好近似多峰分布，我们可以考虑引入潜在变量，形成联合高斯分布来解决这个问题。

条件与边缘高斯分布

两组变量是联合高斯分布，以其中一组变量为条件，另一组变量也是高斯分布。联合高斯分布中任何一个变量的边缘分布是高斯分布。具体证明如下：
在证明之前我们需引入前置知识：

• 假设$\mathbf{x}\sim N(x \vert \mu ,\Sigma)$,我们将$\mathbf{x},\mu$分成两组变量，$\mathbf{x} = (\mathbf{x_a},\mathbf{x_b})$,$\mathbf{\mu} = (\mathbf{\mu_a},\mathbf{\mu_b})$,当然协方差矩阵就被分成了四份：
  
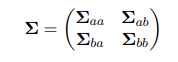
  为表达简单，引入精度矩阵： $$\Lambda = \Sigma^{-1}= \begin{pmatrix} \Lambda_{aa} & \Lambda_{ab} \\ \Lambda_{ba} & \Lambda_{aa} \end{pmatrix}$$ 将多元高斯分布指数上的二项式展开：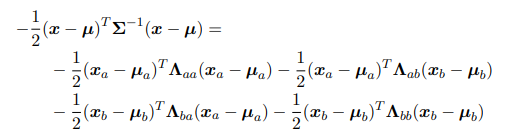
  
  我们注意到一个一般的高斯分布$N(x \vert \mu ,\Sigma)$的指数项可以写成：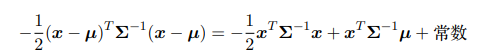
  
  也就是说我们指数项内的变量的二阶项系数就是$-\frac{1}{2}$乘以协方差矩阵的逆$\Sigma^{-1}$，一阶项系数就是$\Sigma^{-1}\mu$。
• 分块矩阵的逆
  
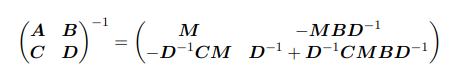
  其中：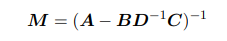
  
  具体推导可以考虑解以下方程： $$\begin{pmatrix} A & B \\ C & D \end{pmatrix} \begin{pmatrix} X_1 & X_2 \\ X_3 & X_4 \end{pmatrix}= \begin{pmatrix} I & 0 \\ 0 & I \end{pmatrix}$$

条件高斯分布

条件高斯分布$p(\mathbf{x_a} \vert \mathbf{x_b})$只需将联合分布中$p(\mathbf{x_a}, \mathbf{x_b})$中的$\mathbf{x_b}$固定为观测值，就是将他看作常数。

$$p(\mathbf{x_a} \vert \mathbf{x_b}) = N(\mathbf{x_a} \vert \mu_{a \vert b},\Sigma_{a \vert b})$$

观察多元高斯分布的二项式展开，$\mathbf{x_a}$的二阶项为：

$$-\frac 1 2 \mathbf{x_a}^T\Lambda_{aa}\mathbf{x_a}$$

所以条件高斯分布$p(\mathbf{x_a}\vert\mathbf{x_b})$的协方差矩阵：

$$\Sigma_{a \vert b} = \Lambda_{aa}^{-1} = \Sigma_{aa} - \Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba}$$

找$\mathbf{x_a}$的一阶项：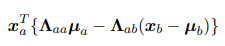

其中用到精度矩阵对称的结论：

$$\Lambda_{ab} = \Lambda_{ba}^T$$

得到条件高斯分布的均值：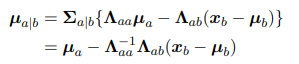

边缘高斯分布

边缘高斯分布$p(\mathbf{x_a}) = p(\mathbf{x_a} , \mathbf{x_b})/p(\mathbf{x_b} \vert \mathbf{x_a})$

$$\begin{aligned} p(\mathbf{x_b} \vert \mathbf{x_a}) &\propto exp(-\frac{1}{2}(x_b-\mu_{b \vert a})^T\Sigma_{b \vert a}^{-1}(x_b-\mu_{b \vert a}))\\ &\propto exp(-\frac{1}{2}(x_b-\mu_b+\Lambda_{bb}^{-1}\Lambda_{ba}(x_a-\mu_a))^T\Lambda_{bb}(x_b-\mu_b+\Lambda_{bb}^{-1}\Lambda_{ba}(x_a-\mu_a))) \end{aligned}$$

找条件高斯分布中指数内关于$\mathbf{x_a}$二次项：

$$-\frac{1}{2}\mathbf{x_a}^T\Lambda^T_{ba}\Lambda_{bb}^{-1}\Lambda_{ba}\mathbf{x_a} = -\frac{1}{2}\mathbf{x_a}^T\Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba}\mathbf{x_a}$$

那我们可以知道边缘高斯分布指数内$\mathbf{x_a}$的二阶项系数等于联合高斯分布中$\mathbf{x_a}$的二阶项的系数减去条件高斯分布中$\mathbf{x_a}$的二阶项系数：

$$-\frac{1}{2}(\Lambda_{aa} - \Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})$$

我们知道精度矩阵是协方差矩阵的逆，那自然精度矩阵的逆就是协方差矩阵。自然有：

$$\Sigma_{aa} = (\Lambda_{aa} - \Lambda_{ab}\Lambda_{bb}^{-1}\Lambda_{ba})^{-1}$$

联合高斯分布二项式一阶项为：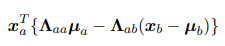

条件高斯分布二项式一阶项为：

$$-\mathbf{x_a}^T\Lambda_{ab}(\mathbf{x_b}-\mu_b) + \mathbf{x_a}^T\Lambda_{ab}\Lambda^{-1}_{bb}\Lambda_{ba}\mu_a$$

边缘高斯分布指数内一阶项系数：

$$(\Lambda_{aa} - \Lambda_{ab}\Lambda^{-1}_{bb}\Lambda_{ba})\mu_a=\Sigma^{-1}\mu_a$$

故边缘高斯分布$p(\mathbf{x_a}) = N(\mathbf{x_a} \vert \mu_a,\Sigma_a)$