贝叶斯多项式拟合

多项式拟合

多项式函数拟合数据：

$$y(x,\mathbf{w}) = \sum ^M _{j=0} w_j x^j$$

误差函数：

$$E(\mathbf{w}) = \frac 1 2\sum ^N_{n=1}(y(x_n,\mathbf{w})-t_n)^2$$

• 拟合训练数据就是找w使误差函数最小，M为多项式阶数。
• M越大，多项式函数越灵活可以更好拟合训练数据，而M过大会产生过拟合的现象，拟合曲线为通过所有训练点剧烈震荡。
  
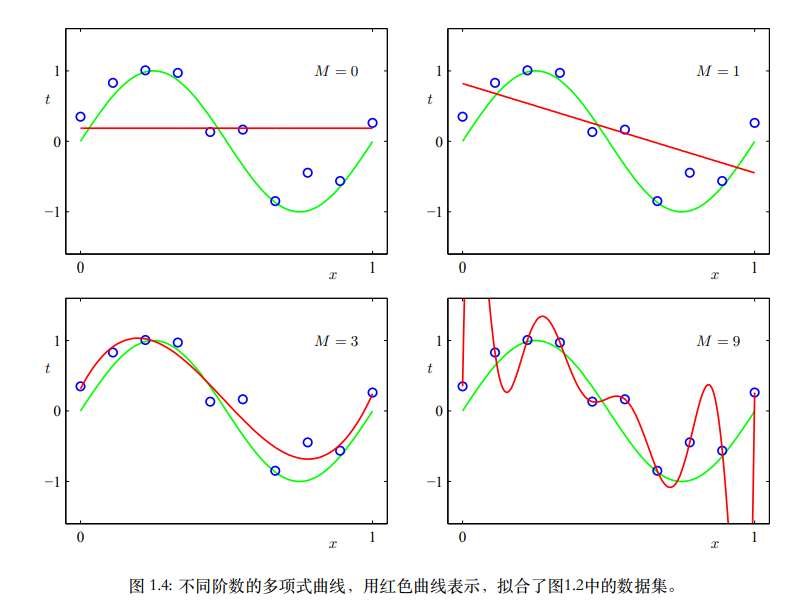
• M过大，系数会被过分调参去拟合训练数据里的噪声，系数值会变得很大。
  
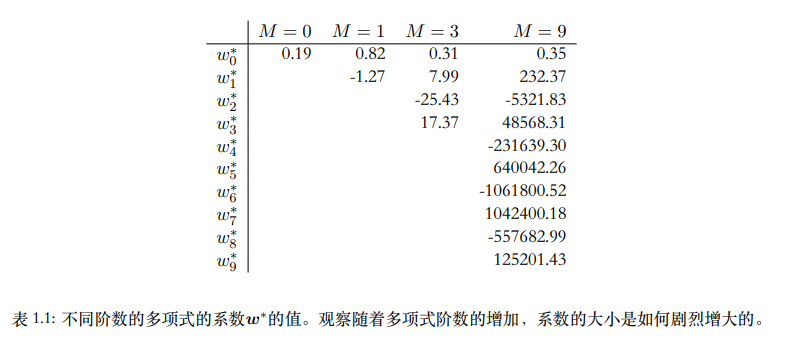
• 所以我们可以通过正则化控制过拟合，即在误差函数中加入惩罚项使得系数不会很大： $$E(\mathbf{w}) = \frac 1 2\sum ^N_{n=1}(y(x_n,\mathbf{w})-t_n)^2 + \frac{\lambda}{2} \|\mathbf{w}\|^2$$

概率论

常见公式

• sum rule： $$p(x) = \int p(x,y) dy$$

• product rule：

  $$p(x,y) = p(x \vert y) p(y)$$

  $p(x,y)$为联合概率，$p(x \vert y)$为条件概率，即Y = y情况下，X = x的概率。

• 贝叶斯公式：

  $$p(\mathbf{w} \vert D) = \frac {p(D \vert \mathbf{w} )p(\mathbf{w} )}{p(D)}$$

  D为观测数据，w为参数。在没有观测到数据时，我们对w有一些假设，以先验概率$p(\mathbf{w})$给出。似然函数$p(D \vert \mathbf{w})$体现观测数据的效果，是w的函数。而$p(\mathbf{w} \vert D)$为后验概率，即表示观测到D后w的不确定性。
  由上面的乘积和求和规则可知：

  $$p(D) = \int p(D \vert w)*p(w)dw$$

  p(D)可以看作归一化常数，故有：

  $$后验 \propto 似然 * 先验$$

  _“在频率学家的观点中，w被认为是⼀个固定的参数，它的值由某种形式的“估计”来确定，这个估计的误差通过考察可能的数据集D的概率分布来得到。相反，从贝叶斯的观点来看，只有⼀个数据集D（即实际观测到的数据集），参数的不确定性通过w的概率分布来表达。”
  我们给定数据集D，没有给w先验要求来寻找合适的w，就是最大化似然函数，是最大似然估计。而如果我们给w一定先验要求p(w)，则是最大化后验估计（MAP）。 如上面提到的平方和误差函数就是最大化似然估计，当给予w一定要求比如说服从0均值正态分布（相当于正则化）就可以得到最大后验估计。 我们可以看到，最大似然估计会产生过拟合的情况，而最大后验估计可以避免过拟合。但是p（w）选取不合适可能导致最大后验估计得到不好的效果。后验估计的另一个好处是，实际应用中我们可能接收到新的训练集D，这时我们就可以把原来的后验分布变成先验分布，然后通过新训练集得到的似然函数更新后验分布。从而可以不断接收新的信息用于解决问题。

高斯分布

一维高斯分布：

$$N(x \vert u,\sigma^2) = \frac {1} {(2\pi\sigma^2)^{\frac 1 2}} exp(-\frac{1}{2\sigma^2}(x-u)^2)$$

u为均值;$\sigma^2$为方差
D维高斯分布：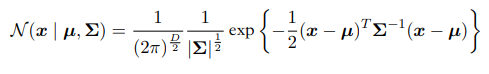

高斯分布在对x积分为1。

$$\int N(x \vert \mu,\sigma)dx = 1$$

此时我们有数据集X，有n个元素x1，x2….xn均从一个高斯分布里抽取，但该高斯均值和方差未知，我们要从数据集里确定这些参数。一般的方法是最大化对数似然函数：

$$p(D \vert \mu,\sigma^2) = \prod ^N_{n=1}N(x_n \vert \mu,\sigma^2)$$ $$lnp(D \vert \mu,\sigma^2) = -\frac{1}{2 \sigma^2}\sum^N_{n=1}(x_n-\mu)^2 - \frac{N}{2}ln\sigma^2 - \frac{N}{2}ln(2\pi)$$

对u求导使之得0，可求得最大似然解：

$$\mu_{ML} = \frac{1}{N}\sum^N_{n=1}x_n$$

同理有方差最大似然解（样本方差）：

$$\sigma^2_{ML} = \frac 1 N \sum^N_{n=1}(x-\mu_{ML})^2$$

但是最大似然方法会系统化低估分布方差，由上可知方差为数据集的函数，我们可以算出样本方差对数据集的期望

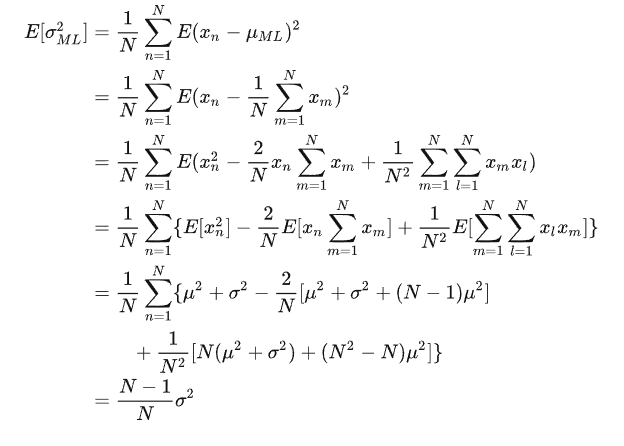
上面推导用到$E[x^2] = var[x] + (E[x])^2 $；a，b独立分布时$E[a*b] = E[a]E[b] $。最大似然偏移问题时过拟合问题的核心。

重新考虑曲线拟合问题

对于训练数据{$\mathbf x,\mathbf t$}，似然函数有

$$p(\mathbf t \vert \mathbf x, \mathbf w,\beta) = \prod^N_{n=1}N(t_n \vert y(x_n,w)，\beta^{-1})$$

实际值为高斯分布，均值为预测值，方差为精度$\beta$的倒数。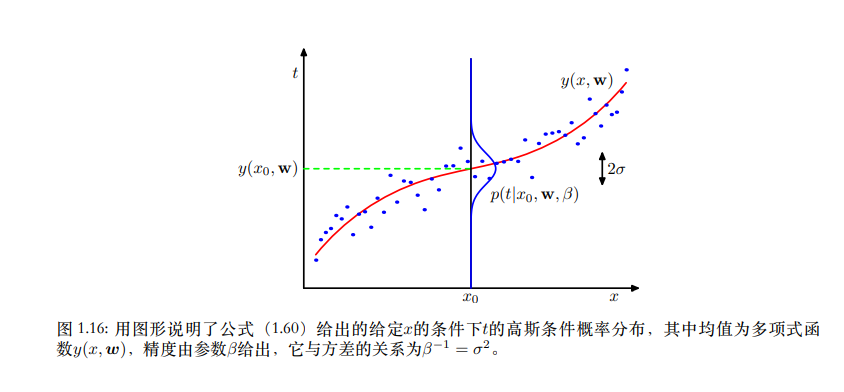

最大似然估计就是找到一组参数w使似然函数最大。我们对似然函数取对数可以发现第一项就是负的平方和误差函数，且只有第一项与w有关。也就是说我们最小化平方和误差函数相当于最大化似然函数。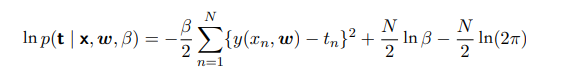

同时我们知道精度$\beta$的最大似然解为下：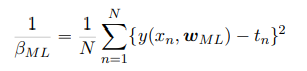

而后我们向贝叶斯迈进一步，考虑w为均值0方差为$\alpha$的高斯分布，意思是让w接近0的概率大点而远离0的概率变小，我们可得先验分布：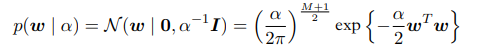

又由贝叶斯公式：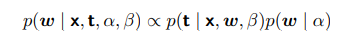

自然可以得到后验概率的负对数中与w有关的项为：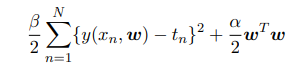

最大化后验概率就是最小化上式，此时等价于最小化上提到的正则化后的误差函数。

贝叶斯曲线拟合

假设$\alpha,\beta$固定。我们之前已经得到$p(w \vert \mathbf{x},\mathbf{t})
$，而后仍然对w进行点估计，这并不是贝叶斯的观点。我们真正要求的其实是预测分布$p(t \vert x,\mathbf{x},\mathbf{t})$。即在给定测试集$\{\mathbf x,\mathbf t\}$同时有测试数据的x这两个条件下，预测t的分布。通过以上公式，我们求出预测分布：

$$p(t \vert x,\mathbf w) = N(t \vert y(x,w),\beta^{-1})$$

此处预测分布可以解析地求出，其可以由高斯的方式给出。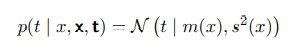

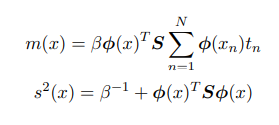
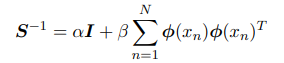
$$\phi(x) = (1,x,x^2...x^M)^T$$

预测分布的均值和⽅差依赖于x，方差表示t的不确定性。
这里给出一种上面解析解的证明方法：

• 我们先解决后验分布部分$p(\mathbf w \vert \mathbf x,\mathbf t)$ $$y(x,\mathbf w) = \mathbf w^T\phi(x)$$ 我们可以知道后验概率的负对数与w有关项为：
  
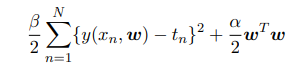
  其余与w无关，故我们可以得到： $$\begin{align*} p(\mathbf w \vert \mathbf x，\mathbf t) &\propto exp(\beta\sum^N_{n=1}(w^T\phi(x_n)-t_n)^2+w^T\alpha Iw)\\ &\propto exp(w^T (\beta\sum^N_{n=1}\phi(x_n)^T\phi(x_n)+\alpha I)w -2\beta w^T\sum^N_{n=1}\phi(x_n)*t_n)\\ &\propto exp(w^TS^{-1}w - 2\beta w^T\sum^N_{n=1}\phi(x_n)*t_n) \end{align*}$$ 后验概率正比与w二次指数项且是归一化的，所以我们可以知道后验概率分布是高斯分布。 $$p(\mathbf w \vert \mathbf x,\mathbf t) = N(w \vert \mu,S)$$ $$S^{-1} = \beta\sum^N_{n=1}\phi(x_n)^T\phi(x_n)+\alpha I$$ $$\mu = \beta S\sum^N_{n=1}\phi(x_n)*t_n$$
• 后续证明需要先引入一个引理：
  高斯相乘引理： 两个高斯函数乘等于一个高斯函数乘上一个常数。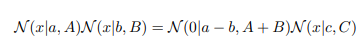
  
  
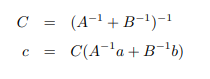
  引理证明方法如下：
  指数部分：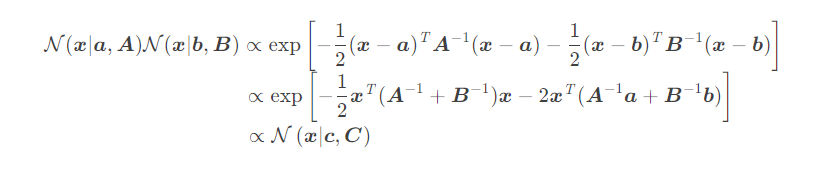
  
  系数部分：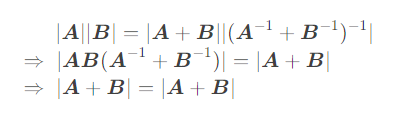
  
  其实就是指数部分相加凑完全平方，剩余的为常数项。同时我们可以通过数学归纳法可以知道多个高斯函数相乘也是高斯函数乘一个常数。
• 让我们回到预测分布：
  
  我们已经知道$p(\mathbf w \vert \mathbf x,\mathbf t)$是高斯的，$p(t \vert x,\mathbf w)$也是高斯的，但是他们两自变量不同故我们需要将后者自变量转为w。 $$\begin{align*} p(t \vert x,\mathbf w) &= N(t \vert y(x,w),\beta^{-1})\\ &= N(t \vert w^T\phi(x),\beta^{-1})\\ &= N(w\vert t(\phi(x)^T)^{-1},\beta^{-1}*\phi(x)^T\phi(x)) \end{align*}$$ 预测分布是对w积分，两个关于w的高斯函数相乘由引理可知为一个关于w的高斯函数和一个常数相乘。关于w的高斯函数对w积分为1，故预测分布等于两个高斯相乘后的常数项。
  即 $$p(t \vert x,\mathbf x ,\mathbf t) = N(0 \vert \mu -t(\phi(x)^T)^{-1},S+\beta^{-1}*\phi(x)^T\phi(x))$$ 将自变量变为t可以得到： $$p(t \vert x,\mathbf x ,\mathbf t) = N(t \vert \phi(x)^T\mu,\phi(x)^TS\phi(x)+\beta^{-1})$$ $$m(x) = \phi(x)^T\mu = \beta \phi(x)^TS\sum^N_{n=1}\phi(x_n)*t_n$$ 预测分布得证。